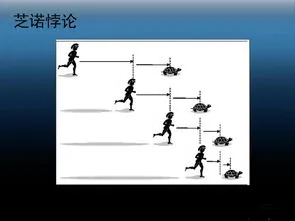
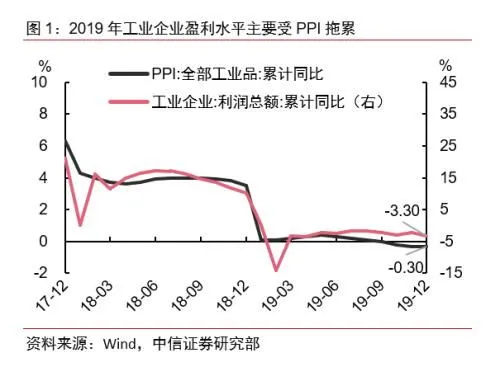
昨天,发表了介绍芝诺悖论和空间连续性的文章《芝诺悖论与空间连续性》。 感谢网友热情的留言参与讨论。 有些解释真的很有启发性。 今天介绍关于芝诺悖论的有趣说明。
芝诺悖论说,阿喀琉斯在阿喀琉斯前面100米,阿喀琉斯的速度是乌龟的10倍,两人同时开始等,永远追不上乌龟。 阿喀琉斯追上前方100米,乌龟已经前进了10米。 阿喀琉斯再追上10米,乌龟又前进了1米,继续这样前进。 阿喀琉斯赶上乌龟原来的位置后,乌龟总是前进一定的距离,阿喀琉斯只能永远跟在乌龟后面。
千百年来,尽管人们对芝诺悖论抱有“诡辩”的偏见,但人们一直试图从多个角度解决这个问题。
例如微积分派从极限和级数的角度来说明,阿喀琉斯追乌龟的点可以无限接近,也就是说极限是有限的,所以在有限的时间内当然可以追上。 但这只是处理了赶上会怎么样,并不是研究能否赶上。 例如,量子力学相当接受宏观微观世界的能量、时间、空间的不连续性,芝诺悖论在一定程度上反映了存在的真相。 但这只是局部的,芝诺悖论还没有完全解释。 唯物主义者的解释基本来自黑格尔,芝诺不懂辩证法,“不知道连续性和间断性的辩证关系,把两者机械地对立起来,从而引起了运动悖论”。 好像什么也没说,好像什么也没说。 可怜的芝诺,连辩证法都不懂到此为止。 难怪一些唯心主义者堂而皇之地接受了芝诺悖论。 一切不过是意识的幻想。
时至今日,严格解释芝诺悖论仍未完全解决,关于芝诺悖论的争论仍在继续。 目前,许多声称解决了芝诺悖论的人可能不了解芝诺悖论的复杂性,也可能是骗子。
在这里,我们将介绍关于芝诺悖论的历史性有趣的说明。 很有启发性。 这就是古希腊犬儒学派的创始人第欧根尼的回答。
第欧根尼的学生教他如何反驳芝诺,但他的老人一言不发,在房间里走来走去,学生还是不明白。 第欧根尼说芝诺不存在运动,但我不是证明了他是错的吗? 这个故事很久以前就被当成笑话了。 很多人相信第欧根尼不理解芝诺的意思。 芝诺并不否认运动现象,但照他说,他可以逻辑证明运动是不可能的,所以我们看到的运动是幻想。 因为,真正的东西一定是合乎逻辑的。
那么,第欧根尼在体育运动中回答的要害在哪里? 是从根本上挑战了芝诺。 是运动的不可能性能否真正用逻辑来证明。
在芝诺悖论中,哪个是第一性的严重问题? 根据芝诺空间连续且可无限划分的假设,他已经把用连续的、数学的运动轨迹代替运动本身作为首要性。 根据后世数学分析对连续性的描述,纯粹的连续性应该是,在任何点上都不存在随后的点; 任意两点之间存在无限的点。 这两种特性都与我们的日常经验相矛盾。 因为前后都被有限的物理事件所确认。 空间连续时,前后在空间结构上找不到依据。 因此,第欧根尼的回答明确了应该恢复运动本身的首要性。
什么意思? 不应该把运动放在时间和空间结构之中,相反,时间和空间结构应该从运动事件中导出。 把运动事件看做第一性,物理点也不再是数学点,阿喀琉斯几步就赶上了乌龟。 放弃了对芝诺空间结构的假设,芝诺问题也不再是问题。 从这一点来看,第欧根尼和芝诺实际上是在挑战空间的连续性,面对数学和物理的对立。
遵循第欧根尼的观点:对运动轨迹的任何分析都不是对运动本身的完整分析,在此基础上既不能也不能证明运动是可能的。 上升到哲学的高度,就是“运动”在“证明”之外,运动是更基本、不可分析的,超越了理性的范畴。 第欧根尼认为芝诺没有证明运动是幻想。 因为这个问题完全不能证明。 因此,第欧根尼一言不发地在房间里飞来飞去的回答并不奇怪。 恰恰相反,非常深刻。
但是运动真的不能证明吗? 只能说不知道。 芝诺悖论引出了这么多问题,选择了物理和数学本质概念上的各种对立。 至今,这些问题仍未得到根本解决。 芝诺悖论长期考验我们的智慧。 今后解决了这些问题,也可能并不最终解决运动本身的问题。 有时必须回顾先贤的思想,钦佩深刻而伟大。
见文章: 《芝诺悖论与空间连续性》